From Kepler to Ptolemy 4

Prev TOC Next

Speed Laws

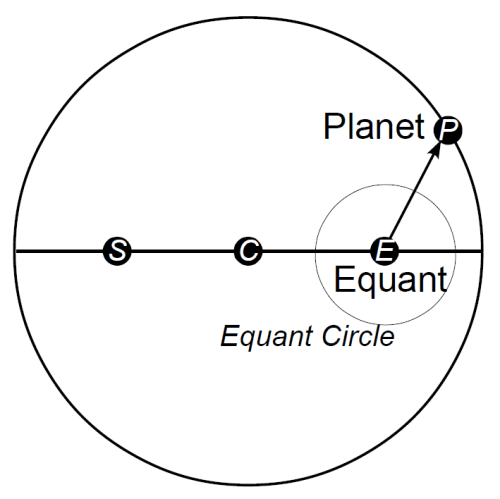
In Ptolemy’s system, the point on the deferent moves uniformly as viewed from a point called the equant point, or sometimes just equant. The equant, the center of the deferent, and Earth all lie in a straight line, with the center midway between Earth and the equant.

Apply this device to the heliocentric model of this figure:

We want the Sun S, the center C of the orbit, and the equant E to lie on a straight line, with the center bisecting the line segment SE. The vector rotates with constant angular velocity, though of course its length changes. Ptolemy did not talk about rotating vectors. Instead he employed an equant-centered circle, with a point moving uniformly on the circumference; he then extended a line from the equant through that point till it intersected the circle¹. The equant-centered circle was called the equant circle, or sometimes just equant, context indicating whether point or circle was intended.

Kepler’s original speed law was inverse distance: the linear speed of the planet was inversely proportional to its distance from the Sun. He introduced his area law as an approximation to this inverse distance law, and eventually realized that the area law was the right one.

We now compare the three laws. The computations get a little too messy for html to handle gracefully, so I’m offloading them to a pdf. Instead I’ll just tell you the variables, make a couple of observations, and jump to the results. (You can safely skip the pdf, if you’re willing to trust me.)

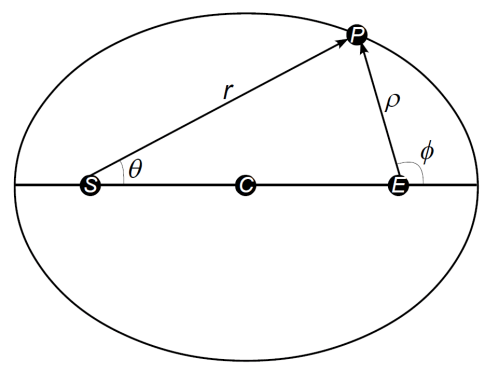
Introduce polar coordinates centered on the Sun, so the planet P has coordinates (r,θ). Also introduce polar coordinates centered on the equant, with P having coordinates (ρ,φ) in this system. Like so:

We will use these coordinates regardless of the shape of the orbit; we’ve illustrated the elliptical case. We let v be the linear speed of the planet, and A the area swept out by the radius vector from some arbitrary initial location.

With the equant speed law, dφ/dt=constant. We write K for this constant: dφ/dt=K.

With Kepler’s inverse distance law, the linear speed is proportional to 1/r. Let K_I be the proportionality constant, so v=K_I/r.

Finally, with the area law, dA/dt is constant; say dA/dt=K_A.

We will compare angular speeds, that is, dθ/dt. This leads to simpler formulas, and also seems natural given the “directional” nature of ancient astronomy.

Before looking at the results, we examine the behavior at the apsides: these are the locations of minimum and maximum distance, r_min and r_max. Let v_min be the linear speed at r_min and likewise for v_max. With all three speed laws

v_min/v_max=r_max/r_min

In other words, at the apsides, speed is inversely proportional to the distance r. So if the speed laws agree at one apside, they will automatically agree at the other.

Our formula holds by definition for the inverse distance law. For the equant and area laws, note that the velocity at the apsides is transverse, with no radial component. So the speed there is v=rdθ/dt=ρdφ/dt. With the equant law, dφ/dt is constant, so v_min/v_max=ρ_min/ρ_max. But ρ_max=r_min and ρ_min=r_max, giving us what we want.

For the area law, the constant rate of increase is dA/dt = ½r²dθ/dt (see the pdf). But v=rdθ/dt at the apsides, as noted, so dA/dt=½vr there. In other words, v_minr_min=v_maxr_max, or v_min/v_max=r_max/r_min, as desired.

Here are formulas for the three speed laws (see pdf):

dθ/dt=Kρr/r2	Equant law for ellipse
dθ/dt=2KA/r2	Area law
dθ/dt=KI/r2	Inverse distance law at apsides

To facilitate comparison, I’ve made the denominator r² in each formula. Focus on the equant vs. the area law for a moment. They won’t agree exactly, because Kρr is not constant and 2K_A is. But for elliptical orbits with small eccentricities, Kρr will be nearly constant. This is because r+ρ=2a, so ρr=r(2a−r), a quadratic with maximum at r=a. If the eccentricity is small, then r_max≈r_min. So r will be close to a, and we’re looking at the relatively flat section of a parabola near the vertex.

Again, if the eccentricity is small, then the velocity is nearly transverse everywhere, and so v≈rdθ/dt everywhere. So dA/dt≈½vr. Therefore if dA/dt is constant (the area law), then the inverse distance law will be nearly true.

We can make a numerical comparison among the laws only once we’ve chosen values for the proportionality constants. We consider two ways to do this. First, we can insist that all three laws give the same speeds at the apsides. This happens if we set K_I = 2K_A = Kr_maxr_min.

Second, we can choose the proportionality constants so that all three laws give the same period T. This seems historically apt, as T is a critical orbital parameter both for Ptolemy and for Kepler.

With the first method, the equant law gives slightly larger speeds than the area law and the inverse distance law slightly smaller speeds.  This follows from our previous discussion with a little thought. Corollary: The equant law gives the smallest orbital period and the inverse distance law the largest.

To study the second method, we express K and K_A in terms of T and the parameters of the ellipse a and b. (Since finding K_I is a pain, we drop the inverse distance law for this part.)

Area law: the rotating r vector sweeps out an area πab in time T at a rate dA/dt = K_A. Thus K_A = πab/T.

Equant law: the rotating ρ vector sweeps out an angle 2π in time T at a rate dφ/dt = K. Thus K = 2π/T.

Again, we put the results in a table:

K=2π/T
dθ/dt=Kρr/r2	Equant law for ellipse
dθ/dt=Kab/r2	Area law

Using the second method, we can also say something about the quadrants: that is, the planet’s location at intervals of T/4, starting with the aphelion (r_max). Consider this figure:

The aphelion occurs at the extreme right. The vertical and horizontal lines through the equant divide the circle into four arcs making right angles, viewed from the equant. So with the equant speed law, those are the planet’s locations at time 0, T/4, T/2, and ¾T.

The vertical and horizontal lines through the circle’s center divide the circular region into four equal-area sectors. But the two dotted regions are pretty close in area. So the two slanted lines, plus the horizontal axis, divide the circular region into four sectors with nearly equal areas. Therefore the times at those four locations will be nearly the same for both the equant and area speed laws.

Okay, now for a graphical and numerical comparison. We use Mars, and the first method for setting  K and K_A. The graph below shows the angular speeds (in degrees per year) for each orbital position from 0° to 180°. Note: the y-axis scale runs from 155°/year to 235°/year; I wanted to stretch the graph vertically to show the difference in the two laws. Angular speed at perihelion is about 45% greater than at aphelion; significant, but not as dramatic as it looks in the graph. (The graph with the other choice of K_A would be quite similar.)

In tabular form:

θ (degrees)	dθ/dt (equant law, °/year)	dθ/dt (area law, °/year)
0	158.9	158.9
30	163.7	163.3
45	169.4	168.6
60	176.9	175.6
90	194.8	193.2
120	212.8	211.5
135	220.2	219.4
180	230.8	230.8

One more remark. To compare the speed laws with observations, we need the delay: how long it takes to get from one position to another. (The total delay around the orbit is just the period T.) Inverting dθ/dt we get dt/dθ, and integrating this between two values of θ we get the desired delay² : delay = ∫_θ0^θ₁ (dt/dθ)dθ. This will matter a lot when we get to Kepler.

[1] Ptolemy actually made his equant and deferent equal-sized; I have drawn the equant circle smaller, which I think is clearer. The size of the equant circle doesn’t matter, of course.

[2] I did a crude spreadsheet calculation (with Δθ=1°), obtaining 1.89 and 1.90 years, respectively, for the Martian orbital period, using the equant law and the area law. The value of T used to set K was 1.88 years.

Prev TOC Next