I’ll begin with Kepler’s first two laws, and work backwards to Ptolemy’s system. Seeing Keplerian astronomy recast this way will expose the bones of the Ptolemaic system.
Deferents and Epicycles
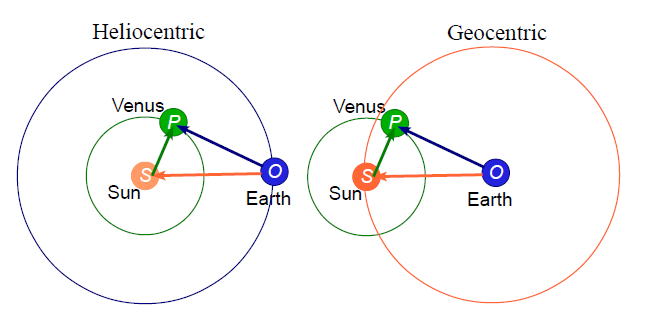
We’ll start with a simpler heliocentric system: the planets travel in circular orbits, at constant speed, centered on the Sun, S. We assume (contrary to fact) that all this takes place in the same plane. We ask, how does the orbit of planet P look from an Earth-centered reference frame? (We use O for Earth, since E has another role to play later.) Take a look:
Consider the moving vector 
We’ve just outlined the basic deferent-epicycle geometry. The planet moves in a circle called the epicycle; its center describes a circle called the deferent. If P is an inner planet (Mercury or Venus), then the deferent is the Sun’s orbit around Earth, and the epicycle is the planet’s orbit around the Sun.
This approach still works for an outer planet (Mars, Jupiter, and Saturn—the others were not known to the ancients). But the epicycle would be bigger than the deferent. We fix this (assuming it needs fixing) with a simple transformation1. Here:
Complete the parallelogram OSPD. We have 
We’ve switched the roles of the deferent and epicycle: the deferent represents the planet’s orbit around the Sun, and the epicycle represents the Sun’s orbit around Earth. However, the centers of these orbits have been moved. (Essentially, we’ve applied the commutativity of vector addition. If 
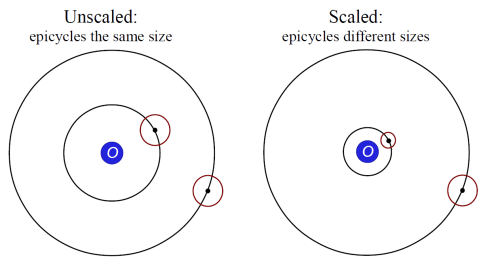
Now a complication: scaling. If we scale up the rotating deferent and epicycle vectors by the same factor, the motion of the planet will look the same, viewed from Earth. After all, only the direction of OP says where P appears in the night sky. The distance affects the brightness, but this was far harder to quantify, especially without telescopes.
Scaling disguises a key fact: all the outer planet epicycles represent the Sun’s orbit. Since Ptolemy scaled the orbits independently for each planet, the epicycles all had different sizes. Thus:
Of course, Ptolemy didn’t know he was scaling the orbits. Rather, with the geocentric approach, nothing forces the epicycles to have the same size.
Since the inner and outer planets switch the roles of deferent and epicycle, this confuses the real state of affairs even further.
[1] Ptolemy actually gives this transformation, showing the equivalence of the so-called “movable eccentric” and “epicycle” models.
Diagonal Argument 
Unfortunately I can’t send my comment on the outside. (About the number of the circles…)
But at least you showed me your blog. Thanks, it is very informative!
You’re welcome!
Feel free to say what you want right here.
“Counting epicycles” has recently popped up on John Baez’s blog Azimuth. Not for Copernicus, but for Ptolemy. I’ll have something to say about that when this series gets far enough.
Gingerich’s assumption is no less hypothetical than Koestler’s. If something is not mentioned in a publication, it may prove that he “didn’t know about it” or “didn’t know Aristarchus because of his heliocentric concept”, and it may also indicate that he “omitted the reference in order to keep something original in his work.” If I had to guess, Gingerich is similarly biased as Koestler, only in the other direction.
I think the outsider Koestler’s opinion is interesting precisely because he endows these stereotypical and/or mythologized heroes with specific features. In a question of this kind (which is far from the most important from my arbitrary point of view), a biography of perverse detail can bring us closer to the solution than general assumptions. For example, Rheticus. I just read in a Kepler volume published a few months ago that he (Rheticus) did not spread the master’s teachings because the Protestants turned away from the heliocentric model. I think Koestler’s psychological, personal explanation is much more convincing. Rheticus simply felt betrayed when he learned that the master didn’t even mention him. Moreover, Koestler’s probably overly negative portrait of Galileo only makes the Italian more interesting and human to me.
In the “Before” and “After” diagram what does symbol D represent? Is it the deferent? What does the larger circle in the “Before” diagram represent? Neither the planet P nor D are on that circle.
Thanks
Russ Potts
In the Before diagram, the large circle is the orbit of Mars about the Sun. It’s the heliocentric version. P is meant to be on that circle; I guess I didn’t draw it carefully enough. I’ve fixed it now.
D is defined as the fourth point of the parallelogram OSPD. As P describes its circular orbit around the Sun, D describes a circular orbit around the Earth. The circle described by D is the deferent, but I drew it only in the After diagram. It is the orbit of Mars shifted left by the vector SO. D therefore doesn’t lie on the large circle in the Before diagram.