We’ve seen the basic plan for an outer planet in post 2:
Author Archives: Michael Weiss
First-Order Categorical Logic 11
MW: Last time we justified some equations and inequalities for our adjoints: they preserve some boolean operations, and “half-preserve” some others. And we incidentally made good use of the color palette!
Filed under Categories, Conversations, Logic
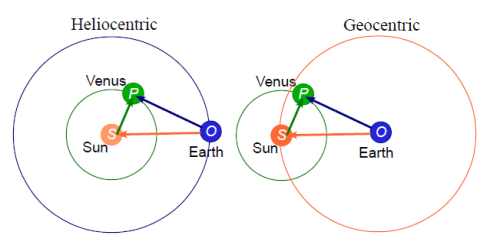
From Kepler to Ptolemy 9
The Moon is the one solar body that does revolve around the Earth. It never displays retrogression. So you’d think Ptolemy wouldn’t “need no stinkin’ epicycles” for it. In fact, Ptolemy gave it a mechanism more complicated than that of any of the planets except Mercury! Here’s the model:
Set Theory Jottings 4. Ordinals
We saw how Cantor introduced ordinals originally as “symbols”,
0, 1, 2,…; ∞, ∞+1, ∞+2,…; 2∞, 2∞+1,…; 3∞,…; 4∞,…
∞2, ∞2+1,…; 2∞2,…; 3∞2,…; ∞3,…; ∞4,…
∞∞,…; ∞∞∞…; ∞∞∞∞…
Filed under History, Set Theory
From Kepler to Ptolemy 7
The Full Ptolemy
We now start the second part of this series: an in-depth look at the Ptolemaic system.
Set Theory Jottings 3. The Paradoxes
Frege added an appendix to volume II of his 1903 magnum opus Grundgesetze der Arithmetik (Foundations of Arithmetic). It began:
A scientist can hardly meet with anything more undesirable than to have the foundations give way just as the work is finished. I was put in this position by a letter from Mr. Bertrand Russell when the work was nearly through the press.
Filed under History, Set Theory
First-Order Categorical Logic 10
JB: Last time we saw how to get some laws of logic from two facts:
• right adjoint functors between boolean algebras preserve products (‘and’),
and
• left adjoint functors between boolean algebras preserve coproducts (‘or’).
Filed under Categories, Conversations, Logic
First-Order Categorical Logic 9
Filed under Categories, Conversations, Logic
Diagonal Argument 