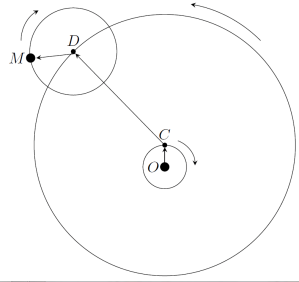
The Moon is the one solar body that does revolve around the Earth. It never displays retrogression. So you’d think Ptolemy wouldn’t “need no stinkin’ epicycles” for it. In fact, Ptolemy gave it a mechanism more complicated than that of any of the planets except Mercury! Here’s the model:
The Moon M is carried on an epicyle with center D. D in turn is carried by a deferent with center C. Finally, the center of the deferent is carried by a small inner circle whose center is the Earth O. The epicycle and inner circle rotate in the opposite direction from the deferent.
The angular speed of C is constant. The angular speed of D is constant as viewed from O; in other words, O functions as an equant. The angular speed of M about D varies, but in a more complicated way than I care to get into.
The parameters are chosen so that whenever OCDM line up in that order, the mean Sun also lies on the same line; likewise whenever COMD line up.
As with the solar theory, we can ask why it differs from our Kepler-to-Ptolemy rule. That would give the Moon an eccentric deferent with an equant governing the speed, and the center of the circle bisecting the eccentricity.
Part of the answer lies with the Hipparchus lunar model, which Ptolemy describes. This has a concentric deferent and an epicycle rotating in the reverse direction: in other words, the figure with the inner circle removed and O and C coinciding. Because the circles rotate in opposite directions, the Moon has its maximum angular speed at perigee and its minimum at apogee. So this can substitute for both the equant and the eccentricity of the deferent.
For the second part of the answer, we skip past Kepler to Newton, and the Earth-Moon-Sun system as an instance of the famous three-body problem—the only topic that “made Newton’s head ache”. The Kepler orbit for the Moon describes its motion only approximately; one must take into account perturbations. Ptolemy’s model reflects the most important of these, which came to be known as evection. So the mean Sun pops up in the model with good reason.
Ptolemy’s model does a good job predicting longitudes, but fails miserably for computing distances from the Earth to the Moon. The apparent diameter of the Moon would vary by a factor of two according to the model; the actual variation is no more than 14%. Ptolemy does not mention this discrepancy.