From Kepler to Ptolemy 8

Prev TOC Next

The Sun

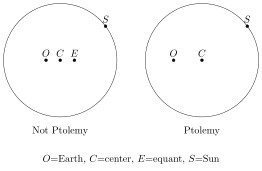
According to the Kepler-to-Ptolemy transformation, Ptolemy should have given the Sun an eccentric circle for its orbit, fitted out with an equant. The line through the Earth and the equant would be the apse, and the center of the orbit would bisect the segment from the Earth to the equant. (See figure below.) This arrangement came to be called “the bisection of the eccentricity”, and it’s the geometry Ptolemy used for all the planets except Mercury.

But Ptolemy opted for a simpler model for the Sun: an eccentric circle with no equant, the Sun moving at a uniform speed. To account for the observed lengths of the seasons, Ptolemy had to assign the Sun an eccentricity twice its actual value. Like so:

Ptolemy’s Solar Model

It’s easy to see why, roughly, by considering angular speeds at apogee and perigee. With the equant speed law, the angular speed at apogee has a “double slowdown” compared to perigee: the point is actually moving slower, and it appears even slower because of the greater distance. With double the eccentricity, the larger distance ratio compensates for the uniform velocity.¹

Why did Ptolemy eschew the equant here? We can only speculate, but Ptolemy explictly credits Hipparchus for the solar model. Hipparchus did not have the equant in his toolkit. Ptolemy may have felt, if it ain’t broke, don’t fix it. Ptolemy did not even update the numerical parameters, although they had changed over 300 years thanks to the precession of the equinoxes.

The mean Sun (S) travels on an orbit concentric with the Earth, with the same period (one tropical year) as the true Sun (S), as in this figure:

Mean Sun and True Sun

Thus it not only moves uniformly, but appears to move uniformly when viewed from Earth. The mean Sun plays an important role in the rest of the Ptolemaic system.

[1] Here are the gory details. As noted in post 4, with all three speed laws

v_min/v_max = r_max/r_min

(Recall that v_min is the speed at r_min, not the minimum speed. Ditto for v_max.) At the apsides, v = ωr (where ω = angular speed).  Thus

ω_min/ω_max = r_max²/r_min²

Referring to post 3, r_max=a+c and r_min=a−c. So ω_min/ω_max = (a+c)²/(a−c)² ≈ (a+2c)/(a−2c) for small c/a, i.e., small eccentricity. So this is the (approximate) ratio of ω_min to ω_max with all three speed laws.

On the other hand, what do we have for uniform speed with double the eccentricity? We double the eccentricity by replacing c with 2c and keeping a the same. Uniform speed means that v_min=v_max, i.e., ω_minr_min=ω_maxr_max. So the ratio is ω_min/ω_max  = r_max/r_min = (a+2c)/(a−2c).

Since the Earth’s eccentricity is small and the ratio at the apsides is (nearly) the same for both models, we can expect that the models are not too far apart for the rest of the orbit.

Prev TOC Next