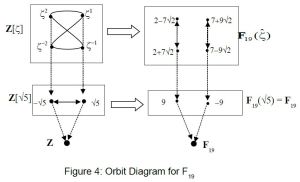
Quadratic reciprocity has hundreds of proofs, but the nicest ones I’ve seen (at least at the elementary level) use Gauss sums. One variant uses the cyclotomic field ℚ(ζ), where ζ is a p-th root of unity. Another brings in the finite fields 𝔽p and 𝔽q.
I wrote up a long, loving, and chatty treatment several years ago, going through the details for several examples. Much longer than the proofs! The diagram up top may give you an inkling.
Anyway, here it is.
Diagonal Argument 